Euclid's Definition, Axioms and Postulates

Euclid's theorem for intersection of two lines states that two distinct lines can not have

Euclid's theorem for intersection of two lines states that two distinct lines can not have more than _____ point in common.

(Note: Write answer in words)

Two distinct lines can have more than one point in common.

Write the number of points common for two different lines.

State and prove Euclid's theorem for the intersection of two lines.

Euclid's fifth postulate does imply the existence of parallel lines.

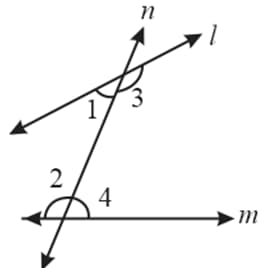
In the above figure, $\angle 3+\angle 4>180°$. If the lines $l$ and $m$ are produced indefinitely they will meet on that side on which $\angle 3+\angle 4>180°$.

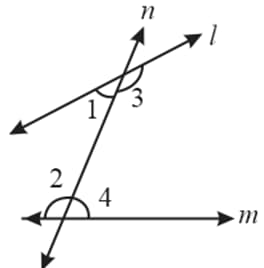
In the adjacent figure,  a line$n$ falls on lines$l$ and $m$ such that the sum of the interior angle$\angle 1$ and $\angle 2$ is less than $180°$.On which side of the transversal $n$ will the line $l$ and line $m$ meet?

State Euclid's fifth postulate. Mention one significance of Euclid's fifth postulate.

A line which lies evenly with the points on itself is called a 

A straight line is a line which does not lies evenly with the points on itself.

Which of these following statement is true.

A straight line is a line which lies evenly with the _____ on itself.

State Euclid's definition of a straight line.

Two distinct intersecting lines cannot be _____ to the same line.

Two distinct intersecting lines cannot be parallel to the same line.

For every line $\text{'}l\text{'}$ and for every point $P$ not lying on $\text{'}l\text{'}$, there exists a unique line $m$ passing through $P$ and _____ to $\text{'}l\text{'}$.. 

Prove Playfair's axiom.

State Playfair’s axiom.

The ends of a line segment are points.